pirámides de Egipto-KEOPS-número áureo.-suceción de Fibonacci-número pi
La construcción de las pirámides de Egipto
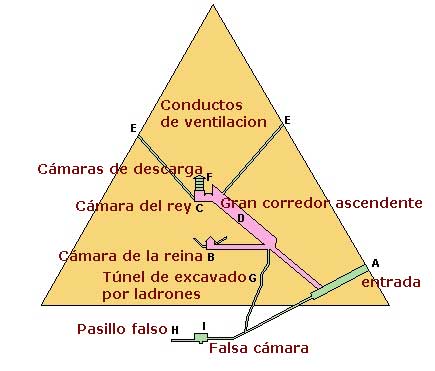
LA GRAN PIRAMIDE DE KEOPS
En 20 años -2.300.000 bloques de piedra de cerca de 2,5 tonelasdas
El misterio de la construcción de la piramide de Keops ¿solucionado?
El título de este post atraerá a gente que se sentirá decepcionada con mi página. La gran pirámide de Giza es la única de las siete maravillas que aún perdura. Sirvió como tumba al faraón Jufu (Keops en griego). Su construcción hace 4500 años siempre ha sido un asunto que ha fascinado a la gente. Tres millones de bloques de piedra de gran tonelaje formando una pirámide cuya construcción se realizó en 20 años según el testimonio de Herodoto.La teoría más extendida es la de una gran rampa utilizada por los egipcios, pero hace 8 años, el arquitecto francés Jean-Pierre Houdin tuvo una intuición y creó una teoría que ha ido desarrollando hasta ahora. Jean-Pierre Houdin afirma haber resuelto el misterio y realizará investigaciones de campo no invasivas para corroborar su teoría. Según esta teoría se utilizó una rampa exterior para los primeros 40 metros y a continuación una rampa interna en forma de escalera de caracol para completar los 146 metros totales.
No son videos sino presentaciones interactivas en 3D. En una de ellas puedes rotar, acercarte, etc. para elegir el punto de vista que más te guste. Dispone de sonido y narración en castellano.
jueves, 16 de septiembre de 2010
La construcción de las pirámides de Egipto
La construcción de las pirámides de Egipto sigue siendo uno de los grandes enigmas de la historia. ¿Cómo se construyeron las pirámides de Egipto?. Se dice que los egipcios no conocían ni la rueda ni las poleas. La Gran Pirámide de Keops cuenta con 2300000 bloques de piedra caliza de entre 2 y 15 toneladas cada uno. Además tiene 230 metros de lado y 146 metros de altura. Fue la mayor construcción en altura hasta la construcción de la catedral de Colonia. La primera pirámide construída fue la pirámide escalonada de Saqqara encargada por el faraón Zoser al arquitecto Imhotep en torno al 2660 a.C. Construida como una mastaba, ha servido de base para el estudio de otras pirámides.Su forma escalonada da pistas de cómo se construyeron el resto de las pirámides. Los bloques con los que se construían las pirámides podían ser de caliza, arenisca, alabastro y granito. Los bloques se cortaban con forma cuadrada o rectangular, y para tallarlos o cortarlos se usaban mazos de madera y cinceles templados de bronce y de cobre. Para el transporte de los bloques desde la cantera al lugar de construcción de la pirámide se utilizaban grandes barcazas que se desplazaban por el Nilo. El primero en hablar sobre el modo de construcción de las pirámides fue Herodoto. Según Herodoto, la pirámide de Keops fue construida en 20 años y con 3000 trabajadores. La pirámide constaba de varias alturas, en las que se situaban las poleas, de modo que una vez que llegaba la piedra a una de esas alturas, la polea la levantaba a la siguiente y así sucesivamente. Pero como no existían herramientas similares en esa época se deshechó esta teoría. También existe la teoría de la construcción de una gran rampa de arena exterior que ascendía desde el terreno hasta el vértice en línea recta. Dicha rampa ocuparía un volumen de arena superior a la propia pirámide y su pendiente sería excesiva para el izado de los bloques. La última gran teoría es la del francés Jean Pierre Houdin , quien afirma que la construcción de la gran pirámide se realizó mediante una rampa interior y en espiral que permitía la construcción simultánea de la pirámide tanto interiormente como exteriormente. En las esquinas se situaba un artefacto que permitía girar los bloques en el aire. El hueco en las esquinas se remataba con posterioridad. Esta teoría sigue sin resolver el acabado final, pues una vez construída la pirámide hay que rematar el espacio de la compleja rampa y de las esquinas y del vértice. La construcción de la rampa interna no deja de tener cierta complejidad constructiva de abovedado de la misma y transporte de los bloques a través de ella.
La teoría del arquitecto gallego Marcos Castro Vilas es mucho más simple e ingeniosa, permitiendo armonizar el acabado interno con el acabado externo sin necesidad de construir complejas rampas interiores ni la utilización de complejos métodos de izado de bloques en altura mediante poleas. Según Marcos Castro Vilas, los egipcios construían primero una pirámide escalonada a la que se subían los bloques a los diferentes escalones mediante rampas. Una vez levantada la pirámide escalonada se iba deshaciendo hacia abajo con la ayuda de la fuerza de la gravedad y sin poleas de izado. Se iban desplazando los bloques hacia abajo sucesivamente, siguiendo un esquema FRACTAL. Se dividía el escalón en tres partes iguales y los bloques de la parte superior se colocaban en el escalón inferior, quedando una pirámide escalonada con escalones más pequeños. Repitiendo de nuevo el proceso de forma sucesiva, como un fractal, se llegaba a formalizar la pirámide escalonada en una pirámide de paredes lisas. De esta forma tan sencilla se construyeron las pirámides de Egipto, sin necesidad de la utilización de ningún tipo de artefacto o de polea mecánica que obligaba a elevar pesados bloques de piedra. Podemos decir que los egipcios se ayudaron de la fuerza de la gravedad para construir sus pirámides, en vez de luchar contra ella. El mejor artefacto a veces es el ingenio.
Hay que tener en cuenta lo que dice Herodoto, según Herodoto, el modo de construcción de las pirámides seguía a grandes rasgos las siguientes fases. Primero se construía una pirámide escalonada, y luego empezando por arriba se iba "puliendo" la pirámide, de modo que la parte inferior fue la última en recibir el acabado final. Este proceso se observa muy bien en esta teoría, cómo primero se construye una pirámide escalonada, y luego se le da forma empezando siempre desde la cúspide hacia abajo. Este dato es muy importante, primero se construye una pirámide escalonada, y después siempre empezando de arriba hacia abajo se le iba dando forma. Este modo de construir es el que transmitió Herodoto.
En el menú de la derecha se pueden visualizar los diferentes pasos de construcción de una pirámide, primer paso, segundo paso, tercer paso, cuarto paso y quinto paso.
PRIMER PASO.jpg)
SEGUNDO PASO
http://www.bing.com/images/search?q=+construccion+de+la+piramide+de+keops&qpvt=+construccion+de+la+piramide+de+keops&FORM=IGRE#view=detail&id=ACA47D87730F267AED95492EB1D27C2DED488B77&selectedIndex=18
El número de oro en el arte, el diseño y la naturaleza
La proporción juega un papel importante en el arte, el diseño y la naturaleza. La relación armoniosa entre las partes y el todo hacen que un objeto pueda producir emociones en quien lo contempla, en quien lo usa.
Y de todas las proporciones, la proporción de oro es la más frecuente.
Si partimos de un segmento y lo dividimos en dos partes, diremos que esa división es áurea si verifica que:
El número designado con letra griega Fi = 1,61803... , es llamado número áureo o número de oro y es la inicial del nombre del escultor griego Fidias que lo tuvo presente en sus obras.
Un rectángulo es áureo si sus lados son proporcionales a 1 y Fi.
Podés dibujar fácilmente un rectángulo áureo siguiendo estos pasos:
1) Dibujá un cuadrado y prolongá uno de sus lados
1) Dibujá un cuadrado y prolongá uno de sus lados
2) Marcá el centro del lado que habías prolongado y con centro en ese punto y tomando como radio la distancia que va de ese punto a uno de los vértices del lado opuesto, trazá un arco de circunferencia hasta que se corte con la prolongación del lado.
3) Usando este punto cerrá un rectángulo que comparta dos vértices con el cuadrado.
Y ya está. ¡Dibujaste un rectángulo áureo!
A partir de este rectángulo se construyen otros semejantes que se han utilizando en arquitectura, pintura y diseño.
En Arquitectura, desde la antigüedad, se ha usado muy frecuentemente la proporción áurea. El primer uso conocido del número áureo en la construcción aparece en la pirámide de Keops, que data del 2600 a.C.
La fachada del Partenón (siglo V a.C.) también refleja está sabia proporción.
En Pintura y Escultura también tuvo su apogeo el
En la primera, se destaca un cuadro de Dalí pintado en 1949. Sintetiza siglos de tradición matemática y simbólica, especialmente pitagórica.
En la segunda, los lados del rectángulo en el cual está idealmente inscrita la estatua del Apolo de Belvedere están relacionados según la sección áurea y en la Venus de Milo observamos también la aparición del número de oro (la altura total dividida la altura hasta el ombligo nos da el número de oro).
| Leda Atómica - Apolo de Belvedere - La Venus de Milo |
Unas proporciones armoniosas para el cuerpo, que estudiaron antes los griegos y romanos, las plasmó en este dibujo Leonardo da Vinci. Sirvió para ilustrar el libro La Divina Proporción de Luca Pacioli, editado en 1509.
En dicho libro se describen cuales han de ser las proporciones de las construcciones artísticas.
Diariamente manejamos objetos en los cuales se ha tenido en cuenta las proporciones áureas para su elaboración. Por ejemplo, la mayoría de las tarjetas de crédito así como nuestro registro de conducir tienen la proporción de un rectángulo áureo. También lo podemos encontrar en las marquillas de cigarrillos, construcción de muebles, marcos para ventanas, camas, etc.
 |
| Hombre de Vitruvio |
Pacioli propone un hombre perfecto en el que las relaciones entre las partes de su cuerpo son proporciones áureas. Estirando manos y pies y haciendo centro en el ombligo se dibuja la circunferencia. El cuadrado tiene por lado la altura del cuerpo que coincide, en un cuerpo armonioso, con la longitud entre los extremos de los dedos de ambas manos cuando los brazos están extendidos y formando un ángulo de 90º con el tronco. El cociente entre la altura del hombre (lado del cuadrado) y la distancia del ombligo a la punta de la mano (radio de la circunferencia) es el número áureo.
En la naturaleza, aparece la proporción áurea también en el crecimiento de las plantas, las piñas, la distribución de las hojas en un tallo, las dimensiones de insectos y pájaros y la formación de caracolas.La suceción de Fibonacci
Consideremos la siguiente sucesión de números: 1, 1, 2, 3, 5, 8, 13, 21, 34, ... Cada número a partir del tercero se obtiene sumando los dos que le preceden (por ejemplo, 21=13+8; el siguiente a 34 será 34+21=55). Esta sucesión es la llamada "Sucesión de Fibonacci". Los cocientes (razones) entre dos números de la sucesión, se aproximan más y más al número de oro (1,61803...). La serie de Fibonacci se puede encontrar también en botánica: ciertas flores tienen una cantidad de pétalos que suelen ser términos de dicha sucesión y cualquier variedad de piña presenta siempre un número de espirales que coincide con dos términos de la sucesión: 8 y 13 ó 5 y 8.
La estrella pentagonal o pentágono estrellado era, según la tradición, el símbolo de los seguidores de Pitágoras. Los pitagóricos llamaban a ese símbolo de cinco puntas pentalfa y consideraban que el 5 era el número de la armonía entre la salud y la belleza, pues era la combinación perfecta del 2 y el 3 (primer número par y primer número impar completo). Pentalfa = pent-alfa (cinco principios) .
La casualidad hizo que en su propio símbolo se encontrara un número raro: el numero de oro.
La estrella pentagonal está por todas partes y representa las cosas más dispares. Es el símbolo de de los artistas en el Paseo de la Fama de Los Ángeles y el símbolo de muchos partidos revolucionarios. También es el símbolo de algunas religiones, sociedades secretas como los Masones, y es protagonista de multitudes de banderas.
La casualidad hizo que en su propio símbolo se encontrara un número raro: el numero de oro.
La estrella pentagonal está por todas partes y representa las cosas más dispares. Es el símbolo de de los artistas en el Paseo de la Fama de Los Ángeles y el símbolo de muchos partidos revolucionarios. También es el símbolo de algunas religiones, sociedades secretas como los Masones, y es protagonista de multitudes de banderas.
Es clásica la forma pentagonal en las construcciones defensivas:
La Villa Farnesio o Palazzo Farnesio es un importante ejemplo de residencia renacentista construida para la familia romana de los Farnesio en Caprarola, Italia.
| Villa Farnese en Roma y la Ciudadela de Pamplona |
Y, por supuesto, en la naturaleza:
La espiral logarítmica
Si tomamos un rectángulo áureo ABCD y le sustraemos el cuadrado AEFD cuyo lado es el lado menor AD del rectángulo, resulta que el rectángulo EBCF es áureo. Si después a éste le quitamos el cuadrado EBGH, el rectángulo resultante HGCF también es áureo. Este proceso se puede reproducir indefinidamente, obteniéndose una sucesión de rectángulos áureos encajados que convergen hacia el vértice O de una espiral logarítmica.
Esta curva ha cautivado, por su belleza y propiedades, la atención de matemáticos, artistas y naturalistas. La espiral logarítmica vinculada a los rectángulos áureos gobierna el crecimiento armónico de muchas formas vegetales (flores y frutos) y animales (conchas de moluscos), aquellas en las que la forma se mantiene invariante.
A lo largo de la historia de las artes visuales han surgido diferentes teorías sobre la composición. Platón decía: es imposible combinar bien dos cosas sin una tercera, hace falta una relación entre ellas que los ensamble, la mejor ligazón para esta relación es el todo. La suma de las partes como todo, es la más perfecta relación de proporción.
MÚSICA y MATEMÁTICA
Se dice que hay matemática en la música, que la música y la matemática están muy relacionadas, pero… ¿Hay matemática en la música? ¿Qué relación existe entre ellas?
Se dice que Pitágoras acuñó la palabra matemática, que significa “lo que es aprendido”. Él describe un sistema que busca unificar los fenómenos del mundo físico y del mundo espiritual en términos de números, en particular, en términos de razones y proporciones de enteros.
Estudió la naturaleza de los sonidos musicales y fue quien descubrió que existe una relación numérica entre tonos que sonaban “armónicos”. Fue el primero en darse cuenta de que la música podía ser medida por medio de razones de números enteros.
Sabemos que el sonido producido al tocar una cuerda depende de la longitud, grosor y tensión de la misma. Entendemos que cualquiera de estas variables afecta la frecuencia de vibración de la cuerda. Pero lo que Pitágoras descubrió, es que al dividir una cuerda en ciertas proporciones, ésta era capaz de producir sonidos placenteros al oído.
Sabemos que el sonido producido al tocar una cuerda depende de la longitud, grosor y tensión de la misma. Entendemos que cualquiera de estas variables afecta la frecuencia de vibración de la cuerda. Pero lo que Pitágoras descubrió, es que al dividir una cuerda en ciertas proporciones, ésta era capaz de producir sonidos placenteros al oído.
Este concepto era una maravillosa confirmación de su teoría. Números y belleza eran uno. El mundo físico y el emocional podían ser descritos con número sencillos y existía una relación armónica entre todos los fenómenos perceptibles.
Platón reconoce la importancia del elemento matemático.
Dice que si a cualquier arte se le quita la aritmética, la medida, y lo pesable, lo que queda no es mucho.
También expresa que a través de la medida y la proporción siempre se llega a la belleza y a la excelencia.
Aristóteles expresa que están equivocados aquellos que claman que la matemática no dice nada acerca de la belleza y la bondad, y que los elementos de la belleza son el orden, la simetría, la limitación definida y que éstas son las propiedades a las cuales la matemática les pone atención. El punto de vista de la filosofía griega estaba inclinado a seleccionar la forma y la proporción como los elementos típicos de la belleza
Leibniz describe a la música como "un ejercicio inconsciente en la Aritmética". Esta afirmación quizás se podría justificar sobre la base de que el músico intérprete cuenta los tiempos del compás cuando comienza a estudiar una obra pero después de un tiempo de tocarla, ya no está contando conscientemente sino que deja fluir la magia de la música. Sin embargo casi todos los "elementos externos" de la música se definen numéricamente: 12 notas por octava; compás de 3/4, 7/8; 5 líneas en el pentagrama; etc.
En 1739, Euler desarrolló una teoría de consonancia basada en la ley pitagórica. Entre más pequeños sean los números que expresan la relación de vibración de dos notas, éstas serán más consonantes. De ésta forma, Euler estableció un criterio de armonicidad de cualquier intervalo o acorde que concuerda con los hechos observados.
Mozart, en 1777, a los escasos 21 años de edad, escribió un "Juego de Dados Musical” para escribir valses con la ayuda de dos dados sin ser músico ni saber nada de composición. Mediante un simple cálculo, utilizando conceptos del Álgebra Superior, se tienen 11 a la 14 valses diferentes, es decir, aproximadamente 3.797.498.335.832 valses diferentes.
Mozart era un aficionado a la matemática y su enorme talento se mostró una vez más. Con este jueguito tan sencillo dejó la imposibilidad de que intérprete alguno pudiera tocar su obra completa o de que alguna compañía de discos la grabara.
Bela Bartok, alrededor de 1915 desarrolló un método para integrar todos los elementos de la música (escalas, estructuras de acordes con los motivos melódicos apropiados, proporciones de longitud, tanto de la obra en general como los de la exposición, desarrollo, reexposición, frases de conexión entre movimientos etc.) basado en la razón áurea.
En 1924 George David Birkhoff retoma unas ideas que había tenido años atrás pero que no desarrolló por dedicarse exclusivamente a estudios puramente matemáticos. Pensó que la melodía dependía del orden de las notas escuchadas por el oído. Le pareció que podrían establecerse unas relaciones de orden, guardadas por las notas, y así poder escoger las mejores melodías. Para él, el problema fundamental de la Estética era el de determinar, para una clase de objetos, las características específicas de las cuales depende el valor estético.
Uno de los proyectos más interesantes que actualmente se desarrollan en este campo es la "Teoría Matemática de la Música" de Guerino Mazzola. Una de las principales metas de esta Teoría es la de desarrollar un marco científico para la Musicología. Si bien la música está enraizada con realidades físicas, psicológicas y semióticas, la descripción formal de las instancias musicales corresponde al formalismo matemático.
Y bien, ¿qué relación existe entre la música y la matemática? Es decir, ¿qué conexión o correspondencia existe?
Hemos visto cómo se han aplicado conceptos matemáticos (provenientes al fin y al cabo de la naturaleza, del pensamiento abstracto del hombre, etc.) al entretenimiento con un juego de dados, a la Estética, a la Composición Musical y a la creación de un lenguaje preciso para la Musicología y la Música entre otros.
Algunos piensan que la Matemática es un juego simple, que sola y fríamente interesa al intelecto. Esto sería el olvidar la sensación de la belleza matemática, de la armonía de los números y las formas, así como de la elegancia geométrica. Esta es ciertamente una sensación de placer estético que todo verdadero matemático ha sentido y por supuesto que pertenece al campo de la emoción sensible. La belleza y la elegancia matemática consiste en que todos los elementos están dispuestos armónicamente de manera tal que nuestra mente pueda abarcarlos, y de eso se trata la música. Si solamente fuera la rutina de aplicar reglas, las combinaciones obtenidas serían exageradamente numerosas, inútiles o extrañas.
LA ESCALA PITAGÓRICA DIATÓNICA
Pitágoras estaba influenciado por sus conocimientos sobre las medias (aritmética, geométrica y armónica) y el misticismo de los números naturales, especialmente los cuatro primeros (tetrakis). Encontró que al dividir una cuerda a la mitad producía un sonido que era una octava más agudo que el original y que cuando la razón era 2/3 se producía una quinta y que otras razones sencillas producían sonidos agradables. Pitágoras no sabía nada de armónicos. El sólo sabía que la longitud de la cuerda
con las razones 1/2 y 2/3 producía unas combinaciones de sonidos agradables y
construyó una escala a partir de estas proporciones
: la Escala Pitagórica Diatónica Mayor (do, re, mi, fa, sol, la, si, do).
El , representado por la letra griega π, equivale a la constante que relaciona el perímetro o longitud de una circunferencia con su diámetro. Se trata de un valor con un infinito número de decimales, cuya secuencia comienza de la siguiente manera: 3,1415926535897932384626433832795028841…Redondeado en 3,1416, pi es un número irracional -no puede representarse de forma fraccional-, frecuentemente utilizado en las matemáticas y en la física, además de en otras disciplinas como la geometría y la trigonometría.Al cálculo de pi se han dedicado millones de horas desde que los antiguos egipcios, allá por el año 1600 a.C, ya concluyeran que existía relación entre la longitud y el diámetro de una circunferencia.Griegos tan insignes como Arquímedes o Ptolomeo experimentaron con polígonos de cientos de lados y circunferencias de decenas de unidades de radio para aproximarse al número pi con la mayor precisión posible. También lo hicieron en China e India, y más tarde en Europa, continente en el que el francés Fabrice Bellard, a principios de 2010, consiguió establecer el record de decimales conocidos de pi en 2,7 billones.
El número pi está presente en muchas de las fórmulas empleadas para hallar longitudes, áreas y volúmenes.
El número pi está presente en muchas de las fórmulas empleadas para hallar longitudes, áreas y volúmenes.
Número π
De Wikipedia, la enciclopedia libre
es la relación entre la longitud de una circunferencia y su diámetro. Es una constante en geometría euclidiana.| Lista de números – Números irracionales ζ(3) – √2 – √3 – √5 – φ – α – e – π – δ | |
| Binario | 11,00100100001111110110… |
| Decimal | 3,14159265358979323846… |
| Hexadecimal | 3,243F6A8885A308D31319… |
| Fracción continua | 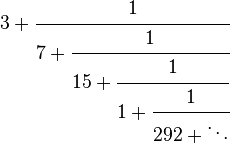 Nótese que la fracción continua no es periódica. |
El nombre π [
Historia del cálculo del valor π [editar]
La búsqueda del mayor número de decimales del número π ha supuesto un esfuerzo constante de numerosos científicos a lo largo de la historia. Algunas aproximaciones históricas de π son las siguientes.Antiguo Egipto [editar]
.png)
.png){kind=small}
Mesopotamia [editar]
Algunos matemáticos mesopotámicos empleaban, en el cálculo de segmentos, valores de igual a 3, alcanzando en algunos casos valores más aproximados, como el de:
Referencias bíblicas [editar]
Una de las referencias indirectas más antiguas del valor aproximado de π se puede encontrar en un versículo de la Biblia:«Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo. Tenía cinco codos de altura y a su alrededor un cordón de treinta codos.»Una cita similar se puede encontrar en Segundo Libro de las Crónicas. En él aparece en una lista de requerimientos para la construcción del Gran Templo de Salomón, construido sobre el 950 a. C.:
I Reyes 7:23-24 (Reina-Valera 1995)
«También hizo un mar de metal fundido, el cual tenía diez codos de un borde al otro, enteramente redondo; su altura era de cinco codos, y un cordón de treinta codos de largo lo ceñía alrededor.»Ambas citas dan 3 como valor de π lo que supone una notable pérdida de precisión respecto de las anteriores estimaciones egipcia y mesopotámica.
II Crónicas 4:2 (Reina-Valera 1995)
Antigüedad clásica [editar]
El matemático griego Arquímedes (siglo III a. C.) fue capaz de determinar el valor de π, entre el intervalo comprendido por 3 10/71, como valor mínimo, y 3 1/7, como valor máximo. Con esta aproximación de Arquímedes se obtiene un valor con un error que oscila entre 0,024% y 0,040% sobre el valor real. El método usado por Arquímedes[5] era muy simple y consistía en circunscribir e inscribir polígonos regulares de n-lados en circunferencias y calcular el perímetro de dichos polígonos. Arquímedes empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.Alrededor del año 20 d. C., el arquitecto e ingeniero romano Vitruvio calcula π como el valor fraccionario 25/8 midiendo la distancia recorrida en una revolución por una rueda de diámetro conocido.
En el siglo II, Claudio Ptolomeo proporciona un valor fraccionario por aproximaciones:
Matemática china [editar]
El cálculo de pi fue una atracción para los matemáticos expertos de todas las culturas. Hacia 120, el astrólogo chino Chang Hong (78-139) fue uno de los primeros en usar la aproximación
, que dedujo de la razón entre el volumen de un cubo y la respectiva esfera inscrita. Un siglo después, el astrónomo Wang Fang lo estimó en 142/45 (3,155555), aunque se desconoce el método empleado.[6] Pocos años después, hacia 263, el matemático Liu Hui fue el primero en sugerir[7] que 3,14 era una buena aproximación, usando un polígono de 96[8] o 192[6] lados. Posteriormente estimó π como 3,14159 empleando un polígono de 3.072 lados.[8] [9]A finales del siglo V, el matemático y astrónomo chino Zu Chongzhi calculó el valor de π en 3,1415926 al que llamó «valor por defecto» y 3,1415927 «valor por exceso», y dio dos aproximaciones racionales de π: 22/7 y 355/113 muy conocidas ambas,[10] siendo la última aproximación tan buena y precisa que no fue igualada hasta más de nueve siglos después, en el siglo XV.[8]
Matemática india [editar]
Usando un polígono regular inscrito de 384 lados, a finales del siglo V el matemático indio Aryabhata estimó el valor en 3,1416. A mediados del siglo VII, estimando incorrecta la aproximación de Aryabhata, Brahmagupta calcula π como, cálculo mucho menos preciso que el de su predecesor. Hacia 1400 Madhava obtiene una aproximación exacta hasta 11 dígitos (3,14159265359), siendo el primero en emplear series para realizar la estimación.[6]Matemática islámica [editar]
En el siglo IX Al-Jwarizmi en su "Álgebra" (Hisab al yabr ua al muqabala) hace notar que el hombre práctico usa 22/7 como valor de π, el geómetra usa 3, y el astrónomo 3,1416. En el siglo XV, el matemático persa Ghiyath al-Kashi fue capaz de calcular el valor aproximado de π con nueve dígitos, empleando una base numérica sexagesimal, lo que equivale a una aproximación de 16 dígitos decimales: 2π = 6,2831853071795865.Renacimiento europeo [editar]
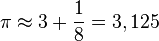
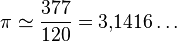
Comentaris
Publica un comentari a l'entrada